In our
last installment, we looked at a sequence of probability density plots of the 2D global ice volume state and inferred that the global climate has undergone changes in organization which we call bifucations.
A reviewer of a recently submitted paper asked why I use a 2D reconstruction when all of the metastable states appear to lie on a line, suggesting that one dimension might be enough.
Let's see what he means.
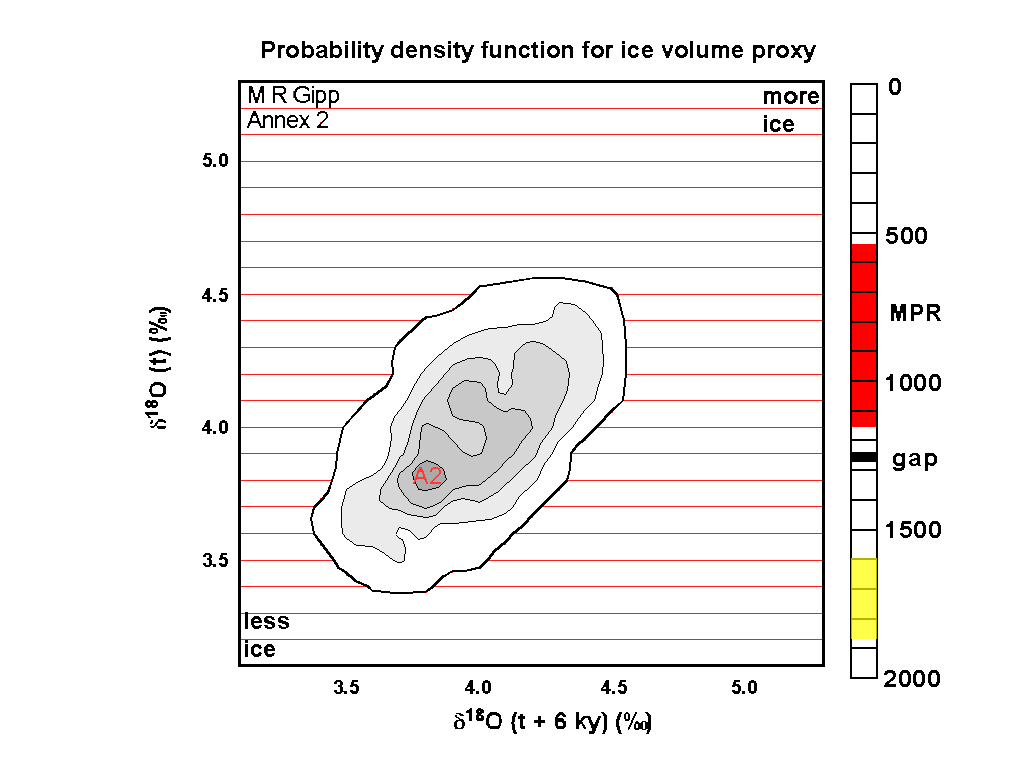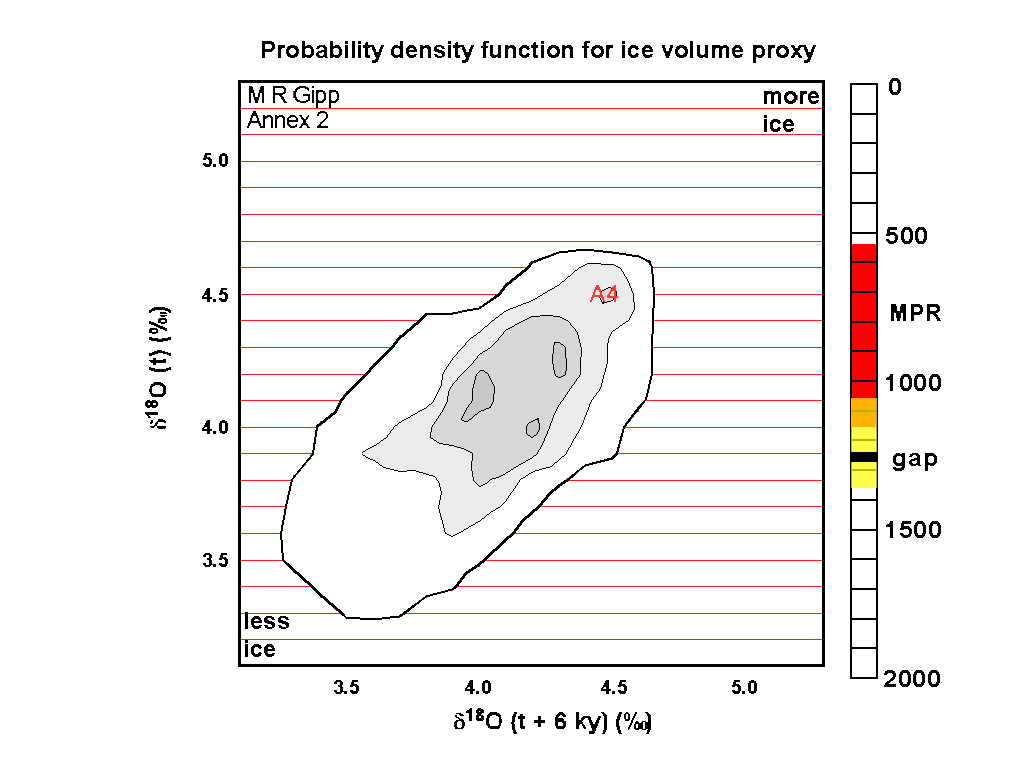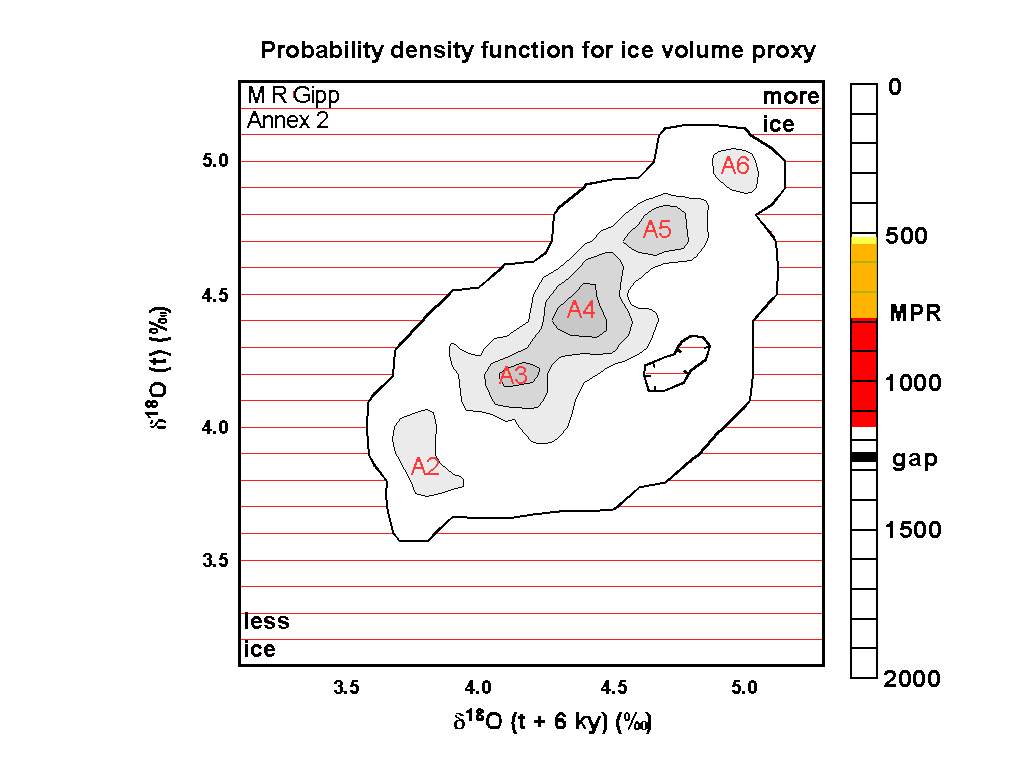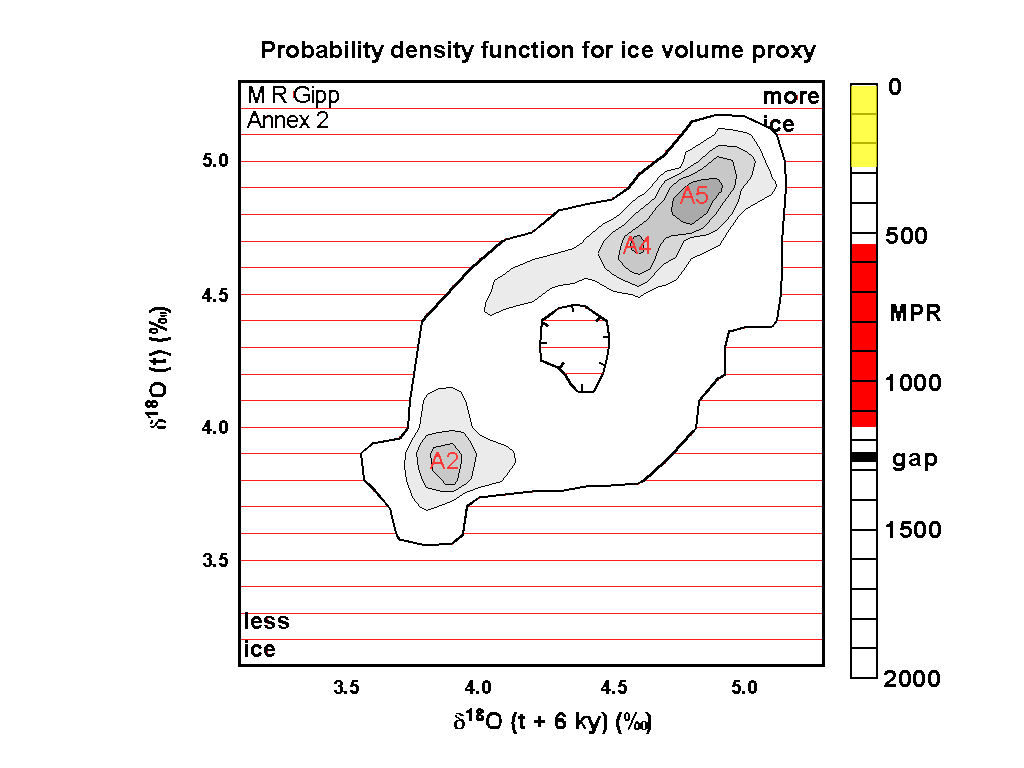
This is one frame of the animation in our last installment. (I suppose this should be Gipp, in rev.) The five Lyapunov-stable areas A2 to A6 all appear to lie on a line, approximately defined by y = x. So do we need two dimensions?
The above is a frame from a poster from the
AGU fall meeting in 2008. The probability density is calculated from the last 750,000 years of the 2-d reconstructed phase space portrait from the ice volume proxy of Shackleton et al. (1990). The curved line is the 2-d phase space reconstruction over the last 125,000 years. At right we see the last 500,000 years of the proxy record.
By inspection we see that for the phase space portrait to plot in the A2 metastable state, the value of the proxy must be between 3.8 and 4.0. This is a necessary condition
but is not sufficient for the state to plot on A2.
Similarly, for the A3 metastable state, the value of the proxy must lie between about 4.1 and 4.3, which is again necessary but not sufficient. To see why, consider the portions of the reconstructed state space near 128,000 years (128 ka), near 68 ka, and near 5 ka (the three blue circles on the reconstructed state space). At all three of these times, the proxy function has values between 4.1 and 4.3, yet none of these points correspond to the LSA--something which would not be obvious purely on the basis of the proxy function.
Such is the hazard of trying to determine the existence of metastable states on the basis of the time series without "unfolding" it into a more appropriate dimension (please note that 2-D is not an adequate projection either, but it does eliminate almost all of this sort of error).
The state space over the interval approximately from 58 ka until about 35 ka plots within the A4 LSA (note blue arrow connecting the appropriate regions on the two plots above). However, at the interval near 11 ka, the proxy function has the appropriate value for the A4 LSA (about 4.6)--nevertheless, the state space does not plot within the LSA, and again provides misleading information if one merely calculated probability density in one dimension.
The reason that the LSAs all line up is due to the
topological equivalence between the two dimensional phase space plotted using the time lag method (as above) with one using the time derivative method. There are types of LSAs that would not plot along the y=x line--in the type of plot we have above we would see two corresponding patches representing the intersection of a toroidal limit cycle with the plane of the plot, each of which would be on opposite sides of the y=x line. The physical meaning of such an LSA would be of an oscillating glacial state--not impossible, but I can't interpret it from the record.
The LSAs A1 to A6 (in the animation) all represent relatively stable global ice volumes--achieved through a kind of dynamic stability that takes into consideration such factors as the slope of the continental shelves, anchoring points on the shelf or in coastal areas and lithospheric and asthenospheric reaction to ice distribution.
Livina et al. (2010) use a one-dimensional approach from a data set to infer the existence of multistability in the climate system over the past 60,000 years using proxies of Greenland temperatures over that interval.This is exactly the problem we are trying to solve (different data set though)!
The basic approach is to find the probability density of the data from the time series (what we have called one-dimensional
here).
A brute force method would be as follows:
Just for fun I'm using a different data set here--this is believed to be a proxy for Himalayan monsoon strength over the past 2+ million years.
To find probability density by a brute force technique, you would draw numerous boxes (yellow) and calculate the length of time the proxy function plots within the box. As the box is slowly migrated from bottom to top, and these different lengths of time are plotted (green wiggle at right--which I have semi-arbitrarily sketched--sorry, I haven't calculated this), you have a probability density plot of the data. This answers the question of whether certain values are more common than others. The more "popular" values may represent metastable states (or Lyapunov-stable areas).
Now, to make things even more interesting you might do what I did in creating the animation in a previous post. Instead of calculating the probability density over the entire data set, you calculate it over a succession of "windows" of time (100,000 years duration, say--the choice depends on what you hope to show). Then you would have a probability density graph for each of these different windows (and there is no reason why the windows couldn't overlap).
If some of your windows had four probability peaks, and others had two or even one, then voila! you have demonstrated a bifurcation.
This is the essence of the argument of Livina et al. (2010). Now, dear reader, if you have been paying attention you will see the problem.
The technique just described overestimates the time spent actually occupying the stable states. To determine how much for the particular data set of Livina et al. (2010) would require some time with the data--which I'm not sure I can spare now.
Livina and her coauthors do not use the brute force method described above. They estimate the probability density using a Gaussian kernel estimator. Okay: I would do the same thing if I had a record as densely sampled as theirs. (There is a two-dimensional estimator that works on the same lines).
They calculate a potential based on the linear probability density estimate and a noise estimate, and approximate the shape of their (linear, remember) potential estimator by a polynomial of even order. The potential estimate [U(z)] has a well (local minimum) corresponding to peaks in probability.
People, people, please. If I've told you once, I've told you a thousand times*--use
Chebyshev polynomials! Seriously. You'll thank me later.
The advantage of orthogonality is key. Chebyshev polynomials are orthogonal whereas standard polynomials are not. (For our purposes, the orthogonality means that the integral from -1 to 1 of the product of two Chebyshev polynomials (say Tn(x) and Tm(x) where m is not equal to n) is zero. Sorry, blogger is crappy at displaying this.
Because of the orthogonality of the individual functions, you can use a Fourier-type process to transform your original function into one composed of Chebyshev polynomials (technically this is a Fourier-Chebyshev transform).
Such a transform has many similarities to a Fourier transform, such as the limitation on the highest-order Chebyshev polynomial (called the Nyquist Chebyshev number) being defined by your sample interval.
Codes for FC transform should be in
Numerical Recipes. They were in the 1989 edition.
Data sets are noisy? Yup! (Paleoclimate sets are notoriously so). You can design filters in the Chebyshev number domain and eliminate some of that unpleasant high-Chebyshev-number noise (like high-frequency noise, only better).
You can also design filters in the Chebyshev number domain, which can be applied to your function without the need for a Fourier-Chebyshev transform by reverse transforming the filter into a series of convolution coefficients and convolving with the original data series. Just as in standard filter design, your filter has to be designed without sharp corners so that the convolution series remains small.
You can define the significance of the different probability peaks in terms of the relative significance of (in the two state case) the fourth order Chebyshev polynomial with respect to the first or second, or of the sixth order polynomial for a three state case.
Livina and her coauthors use a disingenous method of defining the number of wells in their potential function. Since their estimate for the potential is a polynomial of even order, their contention is that the number of wells is better calculated by counting the number of inflection points (where the second derivative is zero--or where the direction of curvature reverses) rather than the number of local minima.
It appears that they may be better off counting both. Here's why.
Here we see a potential function U(z) which is a polynomial of even order. The "+" represent regions of the curve where curvature is positive and the "-" represent segments of the curve with negative curvature.
There are four inflection points in the graph at left. Using equation 7 of Livina et al. (2010), we would infer the presence of three stable states.
By inspection we see only one real potential well, as well as one degenerate solution where both the first and second derivatives are zero. This type of point (just to the left of the origin) is of tremendous significance in dynamic systems analysis, but goes unnoticed by simply counting the inflections.
Compared to the Gaussian kernel estimator, looking at all critical points is a simple matter and is better not overlooked.
The Livina et al. (2010) methodology would be much improved by working in more than one dimension. I have worked in two, but for the data sets I am working on, going to three would be an extremely intense computational exercise. But for data sets with annual sampling over 60 ky or more, going to a three-dimensional probability estimator of the density of points in a three-dimensional phase space would be a huge step forward.
* I know, I know--I've never told you. But I'm telling you now.
References:
Gipp, M. R., 2008. Semiquantitave Characterization of Dynamic Response of Long Records Paleoclimate Records. [damn typos] American Geophysical Union, Fall Meeting 2008, abstract #PP13A-1428.
Gipp, M. R., in rev. Imaging system change in reconstructed phase space: Evidence for multiple bifurcations in Quaternary climate. Submitted to Paleoceanography (in revision).
Livina, V. N., Kwasniok, F., and Lenton, T. M., 2010. Potential analysis reveals changing number of climate states during the last 60 kyr.
Climate of the Past,
6: 77-82. doi:
Update November 14--see a new animation
here